이것저것 잡동사니
[인공지능] 주요 데이터 시각화 그래프 본문
1. 수치형 데이터 (Numerical Data)
1.1 히스토그램 (Histogram)
하나의 수치형 데이터 feature에 대해 데이터의 구간별 빈도수를 나타내는 그래프다.
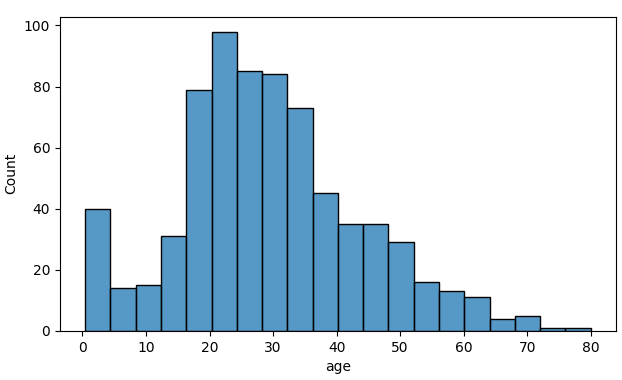
가변 구간 너비(varying-width bins)를 사용하는 히스토그램도 있다. 즉, 하나의 히스토그램 내에서 구간의 너비가 일정하지 않을 수 있다. 데이터의 밀도가 높은 곳에는 좁은 구간을 사용해 밀도 추정의 정확도를 높이고 데이터의 밀도가 낮은 곳에서는 넓은 구간을 사용해 무작위 추출에 의한 노이즈를 줄일 수 있다 (밀도가 너무 낮으면 무작위로 표본을 추출할 시 대부분의 경우 해당 구간에는 데이터가 없는 것으로 간주 될 것이다).

하지만 구간의 너비를 일정하게 하는 것(equal-width bins)이 일반적이다. 이때, 구간의 너비는 다양한 값을 시도해 해당 데이터 분포와 분석 목적에 적절한 값을 찾아야 한다. 물론 다음의 경험적 방법들을 사용해볼 수도 있다. 여기서, \(n\)은 데이터의 개수이며 구간의 개수 \(k\)와 구간의 너비 \(h\)는 다음의 관계를 갖는다.
$$k=\left\lceil{\frac{\max x-\min x}{h}}\right\rceil$$
1) Square-root choice : \(k=\left\lceil\sqrt{n}\right\rceil\)
2) Sturges' formula : \(k=\left\lceil\log_2n\right\rceil+1\)
3) Rice Rule : \(k=\left\lceil2\sqrt[3]{n}\right\rceil\)
4) Shimazaki and Shinomoto's choice :
$$k=\underset{h}{\text{argmin}}\frac{2\bar{m}-v}{h^2}$$
\(\bar{m}\) : 구간 내 데이터의 평균, \(v\) : 구간 내 데이터의 분산
1.2 커널밀도추정 (Kernel Density Estimation, KDE)
간단히 설명하면 히스토그램을 매끄러운 곡선으로 근사한 그래프를 만드는 것이다. 히스토그램과 같은 값(데이터) 분포에서 랜덤한 값을 뽑아냈을 때, 특정 값이 나올 확률을 추정한 것이다. 히스토그램과 형태는 비슷하지만 \(y\)축 스케일이 다른 것을 확인할 수 있다. (확률은 0~1 사이의 값이기 때문)
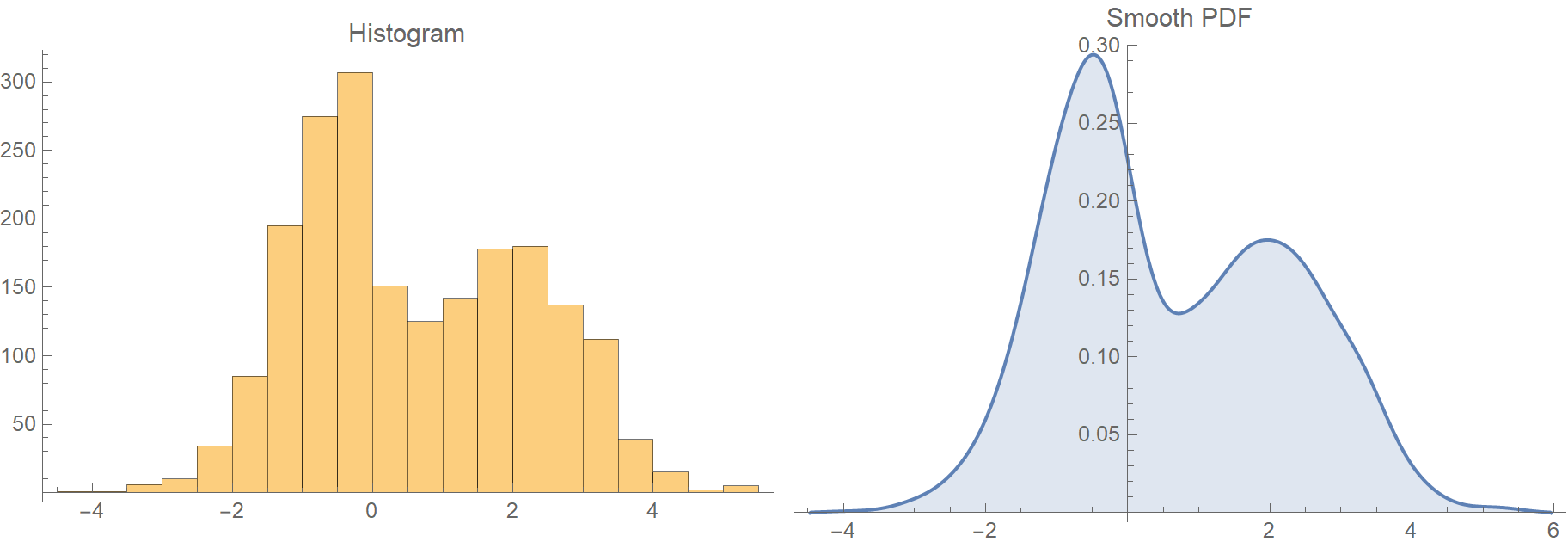
곡선을 생성하는 상세한 과정은 아래의 포스트를 참고하길 바란다.
[수학] 커널 밀도 추정(Kernel Density Estimation, KDE)
커널밀도추정(KDE)은 이산적인 데이터를 사용해 연속적인 밀도함수(density function)를 추정하는 것이다. 간단하게는 히스토그램을 매끄러운 곡선으로 근사한 그래프를 만드는 것이다. 신호 처리
easyselfstudy.tistory.com
1.3 러그플롯 (Rug Plot)
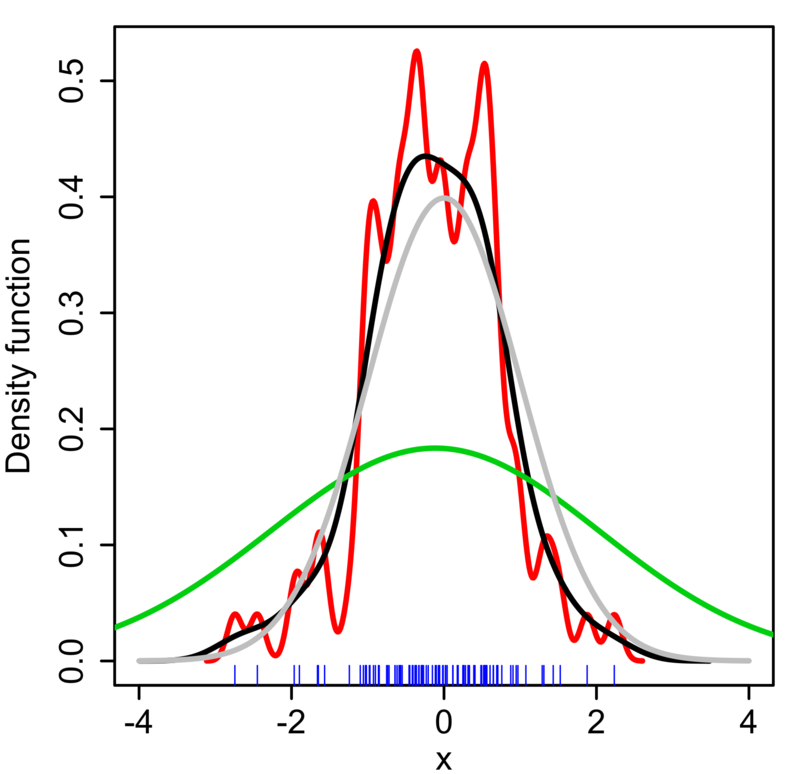
러그 플롯은 축 위에 작은 선분을 그어 데이터의 분포를 나타내는 그래프다. 선분의 밀도가 높으면 데이터 밀도가 높은 영역이다. Zero-width bins histogram 또는 one-dimensional scatter plot이라고도 부른다. 주로 다른 그래프와 함께 사용된다.
2. 범주형 데이터 (Categorical Data)
2.1 막대 그래프 (Bar Chart)
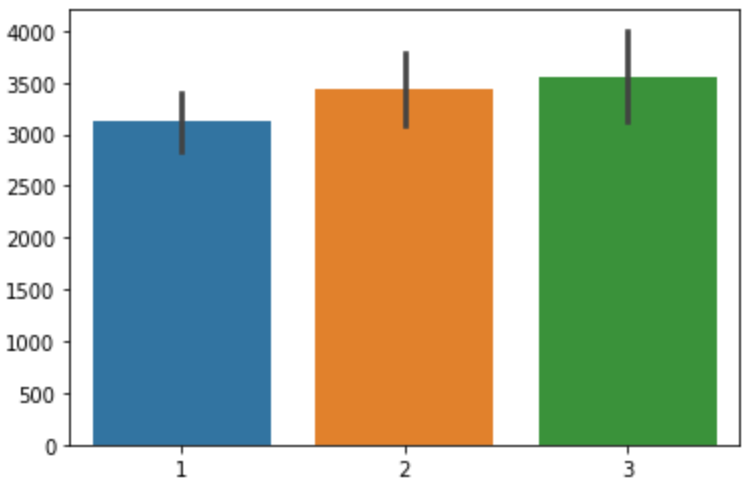
범주에 따른 수치형 데이터 값의 변화를 파악하기 위해 사용한다. 막대의 높이는 해당 범주 데이터의 평균을, 오차 막대(error bar)은 신뢰구간을 나타낸다.
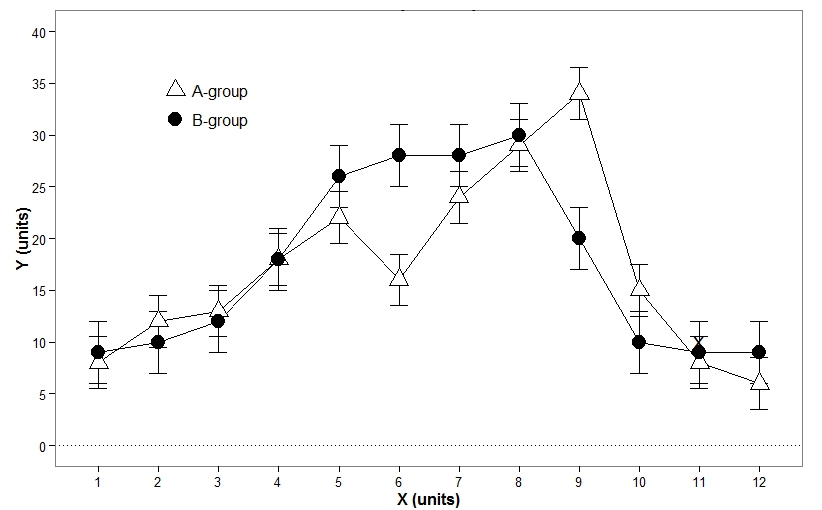
2.2 포인트플롯 (Point Plot)
막대 그래프와 동일한 정보를 제공한다. 한 figure에 여러 그래프를 그려 비교할 때 유용하다.
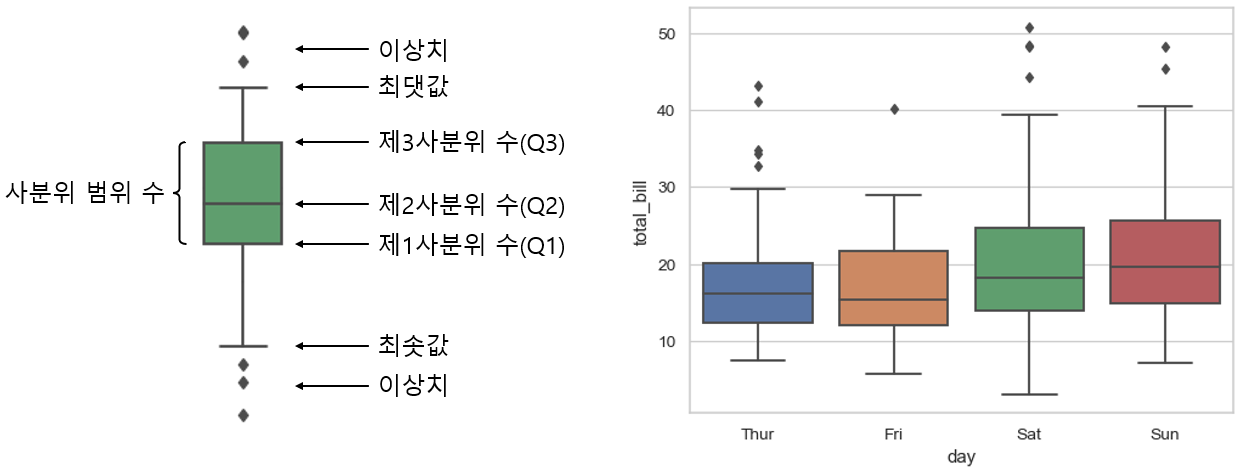
2.3 박스플롯 (Box Plot)
막대 그래프와 포인트플롯보다 더 많은 정보를 제공한다.
- 제1사분위 수(Q1) : 하위 25% 값
- 제2사분위 수(Q2) : 중앙값
- 제3사분위 수(Q3) : 상위 25% 값
- 사분위 범위 수(IQR) : Q3 - Q1
- 최댓값 : Q3 + (1.5 × IQR)
- 최솟값 : Q1 - (1.5 × IQR)
- 이상치 : 최댓값보다 크거나 최솟값보다 작은 값
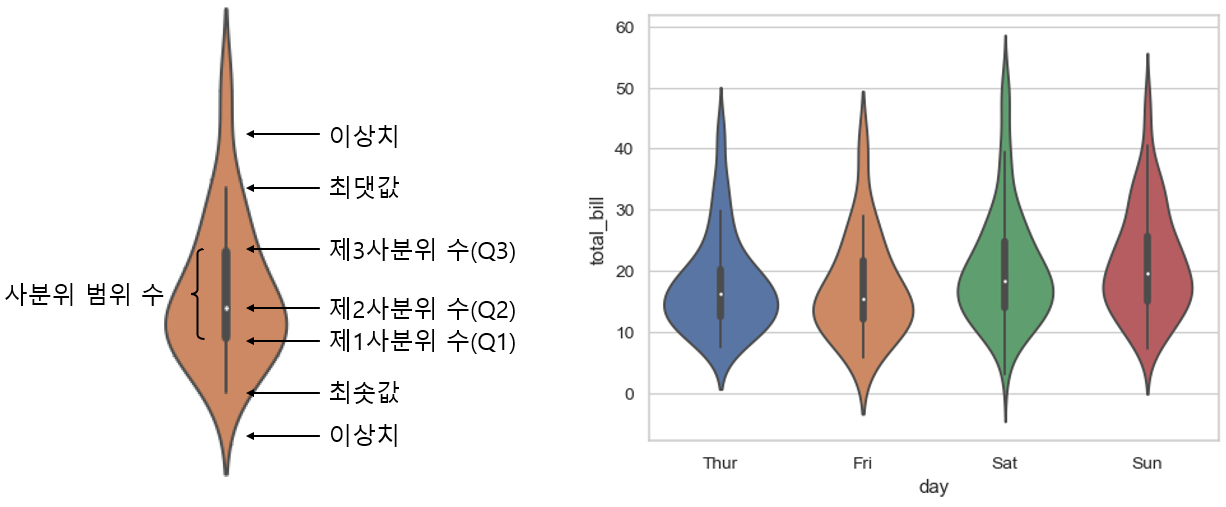
2.4 바이올린플롯 (Violin Plot)
박스플롯과 커널밀도추정 함수 그래프를 합친 그래프다. 데이터의 전체적인 분포를 보고싶다면 박스플롯보다 바이올린 플롯이 더 적합하다.
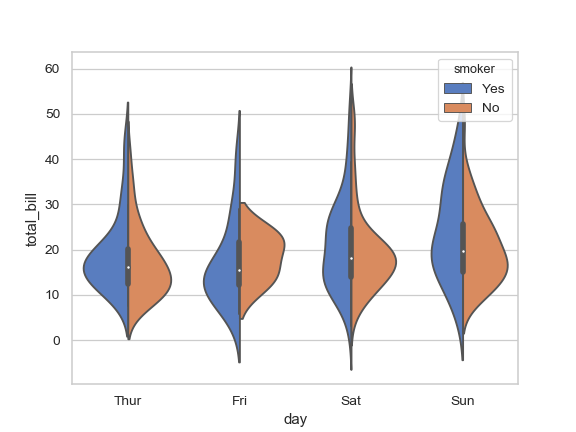
하나의 범주 내에서 다른 두 범주로 나누어 바이올린 플롯을 그릴 수도 있다(split violin plot).
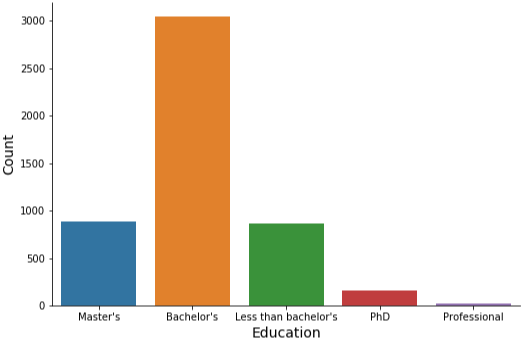
2.5 카운트플롯 (Count Plot)
범주별 데이터 개수를 확인할 때 사용한다.
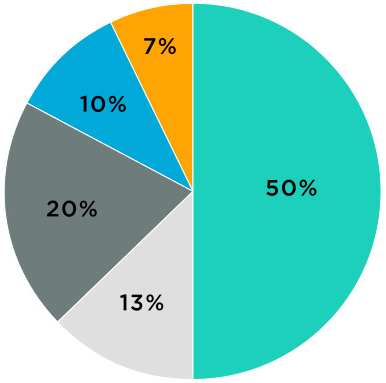
2.6 파이 그래프 (Pie Chart)
범주별 데이터 비율을 알아볼 때 사용한다.
3. 데이터 관계
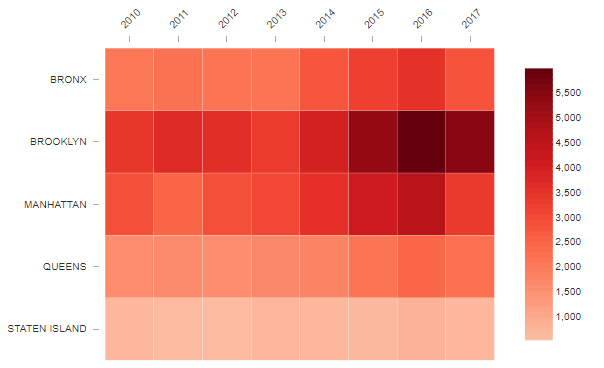
3.1 히트맵 (Heat Map)
두 feature간의 관계를 색상으로 표현한다. 비교해야 할 데이터가 많을 때 주로 사용한다. 수치 데이터로 볼 때보다 의미를 파악하기가 쉽다.
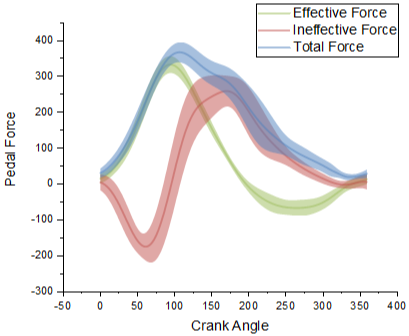
3.2 라인플롯 (Line Plot)
두 feature간의 상관관계를 파악하기 위해 사용한다. \(x\)축의 값에 대한 \(y\)축 값의 평균과 신뢰구간을 나타낸다.
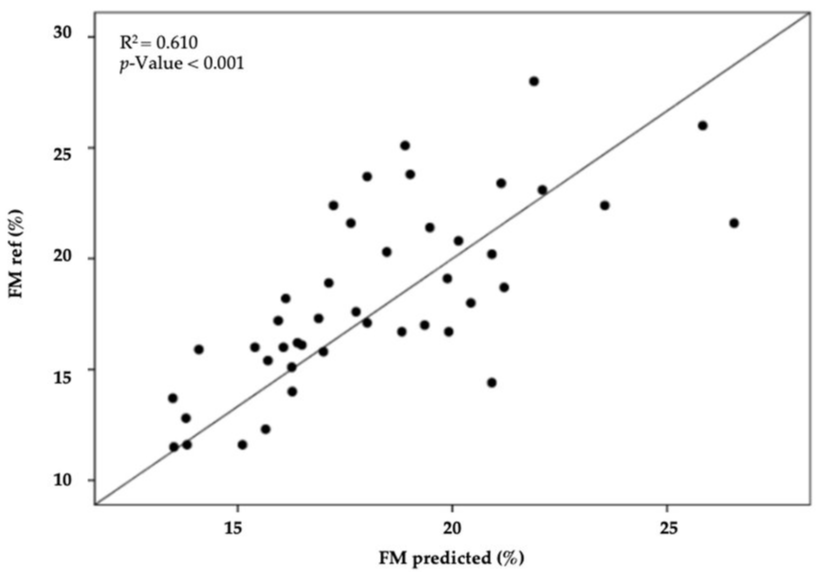
3.3 산점도 (Scatter Plot)
두 feature의 관계를 점으로 표현한다. 선형 회귀선과 함께 사용하면 상관관계 파악이 더 쉽다.
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| [인공지능/머신러닝] 결정 트리(Decision Tree) (0) | 2022.07.22 |
|---|

