[전자기학] 1.1 Vector Algebra

1.1.3 Triple Products

(i) Scalar triple product(스칼라 삼중곱)

$$\mathbf{A\cdot\left(B\times C\right)}=\mathbf{B\cdot\left(C\times A\right)}=\mathbf{C\cdot\left(A\times B\right)}$$

   다음이 성립한다.

$$\mathbf{A\cdot\left(B\times C\right)=\left(A\times B\right)\cdot C}$$

 

(ii) Vector triple product(벡터 삼중곱)

   BAC-CAB rule 이라고도 한다.

$$\mathbf{A\times\left(B\times C\right)=B\left(A\cdot C\right)-C\left(A\cdot B\right)}$$

---

1.1.4 Position, Displacement, and Separation Vectors

   Position vector(위치 벡터)와 displacement vector(변위 벡터)의 개념은 일반물리학에서 배웠을 것으로 가정하고 생략한다. Infinitesimal displacement vector(미소 변위벡터)는 \(\left(x, y, z\right)\)에서 \(\left(x+dx, y+dy, z+dz\right)\)로의 벡터이며 다음과 같다.

$$d\mathbf{l}=dx\,\hat{\mathbf{x}}+dy\,\hat{\mathbf{y}}+dz\,\hat{\mathbf{z}}$$

   Separation vector(분리 벡터)는 position vector에서 source vector(근원 벡터)를 뺀 벡터이다. Source vector는 전기장과 자기장이 만들어지는 근원인 전하와 전류의 위치벡터라고 생각하면 된다. 즉, 전하 또는 전류의 위치에서 공간의 특정 위치까지의 벡터다.

 

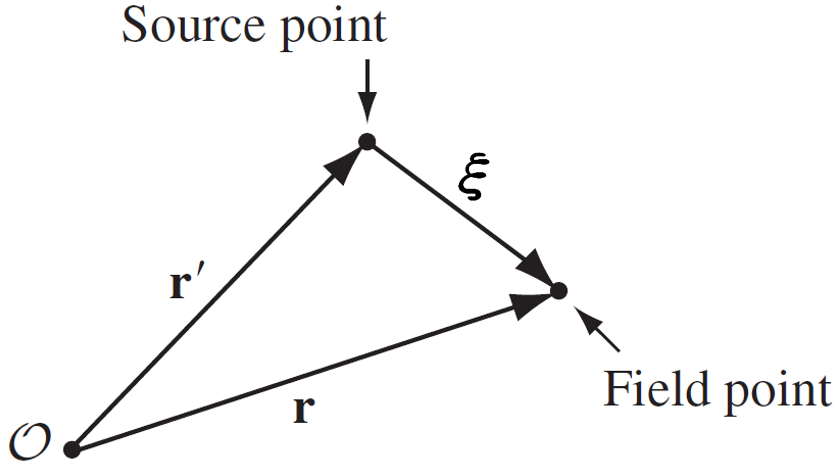
   교재에서는 script-r으로 separation vector를 표기한다. 하지만 해당 폰트는 블로그에 작성하기 어려우므로 그리스 문자 xi(\(\xi\))를 대신 사용하겠다.

$$\boldsymbol{\xi}\equiv\mathbf{r}-\mathbf{r}'$$